This is a simple problem, probably around C for cf div2
오늘 여유가 있어서 백준에서 그래프 문제를 풀었는데…
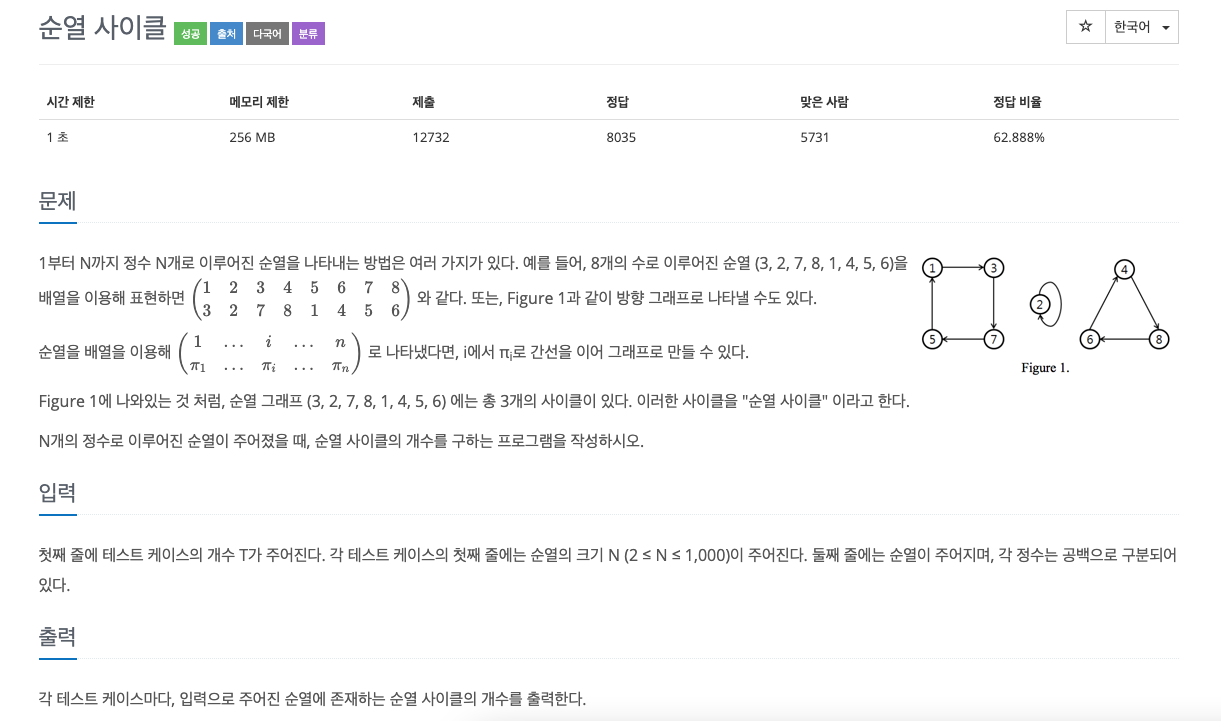
일단은 상대적으로 간단하게 풀 수 있는 문제이다. dfs 기본 구현을 통해 사이클을 구하는 문제다.
한 노드가 두 순열 사이클에 포함된다면?
문제의 조건상 말이 안 된다. 각 노드는 다른 한 개의 노드로만 연결된다. permutation에는 정의상 중복이 없다.
사이클이 없는 경우?
이 문제에서는 사이클이 무조건 존재한다. 존재하지 않는 경우를 만들려고 해도 모든 노드는 다른 노드에서 갈 수 있다. 사이클이 존재하지 않는다면 모든 노드가 자식 노드가 있을 수가 없다.
경로는 사이클이 아닌데 사이클이 포함될 경우?
이슈가 생기는 게 여기였다. 물론 원문에서는 순열에는 중복이 없어야 한다는 예기가 없어서 조건을 성립한다고 생각했었다…
중복이 가능하다면:
Case 1:
[1 2 3 4 5 6]
[2 4 2 5 6 3]
Case 2:
[1 2 3 4 5 6]
[2 4 2 5 6 1]
이 두 가지 경우는 그림을 그리게 되면 엄연히 같다. 하지만 다른 분들의 코드 (ac가 된 submission)들에다 이 값을 넣게 된다면, 1, 2이라는 값을 출력하게 된다.
여기서 사이클의 정확한 정의를 이용하면, 답은 1, 1이 되어야 한다. 1 -> 2 -> 4 -> 5 -> 6 -> 1 에서 3 -> 2 -> 4 -> 5 -> 6 -> 1은 사이클이 아니다. 중복되는 2가 시작점인 1이 아니기 때문이다.
2 -> 4 -> 5 -> 6 -> 3 -> 2도 마찬가지로 1 -> 2 -> 4 -> 5 -> 6 -> 3 -> 2 -> 1은 사이클이 아니다. 중복되는 2가 시작점이 1이 아니기 때문이다.
답 1, 2가 맞다고 해도 말이 안 되는 다른 이유는 두 그래프는 단지 1번과 3번 노드만 변경 했을 뿐이다. 사실상 같은 그래프인데, 사이클 수가 다를 수가 없다. 다른 값이 나오는 이유는 오직 dfs로 1번부터 차례로 돌리므로 [2 4 2 5 6 3]인 경우에는 3이 이미 통과 되기 때문에 3으로 시작하는 사이클은 배제된다.
하지만 [2 4 2 5 6 1]인 경우 i = 1 일 때 3은 포함되지 않음므로 i = 3 또한 성립이 된다.
또한
[1 2 3 4 5 6 7]
[2 4 7 5 6 3 2]
이 경우에도 같은 논리로 의하면 답이 3 이여 한다 (1 에서 시작, 7 에서 시작, 3에서 시작)
물론 설정상 permutation의 정의에 의해 (!중복) 이런 반례가 없어진다. 다른 말로는 저처럼 실수 하지 않는 의미로 permutation이라고 주어지면 까먹지 않는게 좋을거 같다. 다만 중복이 생긴다면 이런 반례가 있다.
심지어 밑에 제가 적은 코드도 ac가 되었는데… 위 두 케이스에는 0, 1이 나온다. 이 코드도 사이클의 정의를 이용하여 구현했기 때문에 1, 1 이 나와야 하는데 위에 같은 반례에 이해 (1일 때 3이 포함되지 않는 경우) 문제가 생긴다. 하지만 이 문제 테스트 케이스를 통과 한 다음에 고칠 마음이 별로 안 든다…
뭐 그냥 dfs를 이용해서 풀면 되는 문제를 (chk를 이용하면서 시작점과 종착점이 같은지 확인 하려고 했다, 중복이 없다면 이럴 필요가 없다)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <bits/stdc++.h>
#define IOS ios_base::sync_with_stdio(0); cin.tie(NULL);
#define ll long long
#define MAX 1e9+1
void IO(string inpt) {
freopen((inpt+".in").c_str(),"r",stdin);
freopen((inpt+".out").c_str(),"w",stdout);
}
#define so(x) sort(all(x))
#define rev(x) reverse(all(x))
#define all(x) begin(x), end(x)
#define del(x, i) erase(begin(x)+i)
#define sz(x) (int)(x).size()
#define pb push_back
#define rem(x, i) erase(begin(x), begin(x)+i)
#define mp make_pair
#define sec second
#define fir first
#define ins insert
#define ez erase
#define MOD 1e9+7
#define MAX_INT 1e18*9
using namespace std;
vector<int> graph[MAX];
bool visited[MAX];
bool dfs (int x, int st, int chk) {
if (chk == 1 && x == st)
return true;
if (!visited[x]) {
visited[x] = true;
for (int i = 0; i < graph[x].size(); i++) {
if (dfs (graph[x][i], st, 1))
return true;
}
}
return false;
}
int main() {
IOS
int t; cin >> t;
while (t--) {
int n; cin >> n;
int arr[n];
memset(graph, 0, sizeof(graph));
fill(visited, visited + MAX, 0);
for (int i = 0; i < n; i++) {
cin >> arr[i];
graph[i+1].pb(arr[i]);
}
int ans = 0;
for (int i = 1; i <= n; i++) {
if (!visited[i] && dfs(i, i, 0)) {
ans++;
}
}
cout << ans << "\n";
}
}